Like, random
(And mostly wrong)
“Nobody knows what I’m going to do”
[Donald Trump, 18 June 2025, talking about Iran ]
as he drags America into yet another unwanted war
Some years ago, I needed a source of randomness a bit more reliable than the current US president. I wanted to anonymise some data properly. So I built my own random number generator (RNG) from scratch. In this post I’ll show you how to do this, something that may seem a bit quixotic, excessive or paranoid. Likely all three.
To compound my folly, I’ll do a lot more. Along the way, we’ll bump into a criminal or two. We’ll meet the man who invented the ‘bit’. We’ll explore why true random is hard to get, and how we can often fill in with pseudorandom instead. Mostly. But why this fascination with randomness? What is it even good for?
Randomness powers our daily life. Every secure connection and pretty much every secret made and kept today depends utterly on nobody being able to guess even a substantial part of an underlying random number! Cryptographic security depends on ‘guess-resistant’ random numbers. This may seem like a bold statement, so let’s explore a bit.
When randomness fails, we have a looming disaster. Think of each random number used to create a secure message as a unique password. If it’s easily guessed—Jamie Tartt in Ted Lasso saying “I did think I’d fooled them by spelling ‘PASSWORD’ with two esses”—then you’re done. Compromised. Finished.
For example, in 2013 every single Android device had a flaw in the underlying Java SecureRandom class. This in turn made every Android-based Bitcoin wallet potentially vulnerable to theft. Technically, random numbers were easily guessed because the system PRNG wasn’t being set up properly; in just a moment we’ll explore what this means. Fortunately, three smart Koreans (Soo Hyeon Kim, Daewan Han and Dong Hoon Lee) were alert, and spotted the defect before too much was stolen. You snooze, you lose.
( Trump needing to be woke at his birthday parade—as noted internationally)
Pseudorandom
Contrary to appearances, this post is not a political diatribe. Well, not much.
Superficially, if you look at the stuff coming out of the mouth of the current US President, it may seem pretty random. But if you step back, then you’ll realise that all of his output is rather predictable frontal-lobe stuff: rants about imagined grievances, self-promotion at the expense of absolutely everyone else, and past infatuations (gilt, Putin, and tariffs). And saying asinine things like the quote at the start of my post, immediately after you’ve effectively declared war on Iran by demanding surrender. In what circumstance other than total war do you demand “unconditional surrender”? </rant>
Similarly, although it initially seems random, the output of a pseudorandom number generator—often called ‘random’ in the less reputable computer literature—is in fact entirely predictable. If you can work out precisely how such a ‘PRNG’ is set up, you can determine future and past values. That’s why it’s so important in cryptography to make sure that you:
Properly obtain and hide the initial, true random number used to initialise (seed) the PRNG.
Don’t just use any old PRNG: use one that is cryptographically secure so that you can’t work backwards to the underlying random number (a ‘CSPRNG’).
Trust nobody more than you absolutely have to (even, it seems, NIST
<sad face>)
A pseudorandom number generator only seems random. Generally, in most computer languages, if you ask for RANDOM, you’ll get pseudorandom.
Then there were three
This is not easy stuff. Cryptography is never easy. Here’s another example of pure badness. The US National Institute of Standards and Technology should in theory be beyond reproach when it makes recommendations. It provides measurement (metrology) standards. We’ve already explored this topic in depth. NIST also provides cryptographic standards, like NIST SP 800-90A, their Recommendation for Random Number Generation Using Deterministic Random Bit Generators. Which are actually PRNGs, specifically CSPRNGs.
When published in 2006, this standard had four ways of making CSPRNGs. In 2014, one of these—Dual_EC_DRBG—was withdrawn. Why? Because in 2013, the New York Times revealed what smart cryptographers already suspected. The United States’ National Security Agency built a back door into the standard, allowing them easy access to any exchange of secrets that used this method. To their credit, NIST belatedly pulled Dual_EC_DRBG. But this does sully them a bit.1
Properly done, a CSPRNG is actually pretty solid. The stream of values coming from it seems pretty random, and the underlying seed should be inaccessible.
The state of PRNGs
Because PRNGs are ultimately entirely predictable, on their own they are useless for keeping secrets. But even insecure PRNGs are not without use. You just need to know where they are useful. For example, in 1953 Nicholas Metropolis (cool name!) and a few other smart people wrote a paper that describes how you can randomly draw samples from pretty much any statistical distribution you can imagine.
With a bit of tweaking, this “Markov-Chain Monte Carlo” (MCMC) approach is hugely useful in physics, and also wherever people do Bayesian modelling. In a recent post, we learnt a bit of simple Bayes—that given prior information and new information (a measure of likelihood), we can create posterior information that edges us into making a sensible decision. We used a lies-to-children approach, and did not explore the general case where we need to build a posterior distribution, given a prior distribution and a function that describes likelihood. The MCMC approach is one way of doing this, and it’s powerful.2
As we already know about the seed, we need just one more concept. In actually building a PRNG, we generally remember its state. For example, in 1997 Makoto Matsumoto and Takuji Nishimura came up with the Mersenne Twister. As the name suggests, this PRNG is usually built from the huge Mersenne prime, 219937 − 1. This corresponds to 19,936 internal ‘state’ bits that change as we move along.
About a decade ago, had you asked me for a good PRNG, in my ignorance I’d have recommended the Mersenne Twister—still used in 2025, by default, in the standard C++ library’s <random>, Python’s random, R, Excel, Stata, GNU Octave, Ruby, and so on. It jumps around nicely and only repeats after 2lots steps. What more could you require?
Quite a lot, it turns out. Now, we know better. Not only is the state bulky at about 2.5 kilobytes, but Mersenne has other undesirable qualities. We now have generators with smaller state and far better behaviour, like those of Melissa O’Neill’s PCG family.3
Practically random
You can get horribly lost arguing about randomness. In a moment, we’ll learn about entropy and how it relates to randomness, but first, let’s build a practical random number generator. My true random number generator. It’s pictured above.
There are three main ways that you can obtain truly random data:
If you have a chunk of radioactive material and a detector. Radioactive decay is, as far as we know, utterly random.4
From background noise, for example radio noise, or the random stuff that’s happening in a computer enclosure.
Noise from an electronic circuit.
The first is usually expensive and—at the end of the day—radioactive; the second may be vulnerable to a clever hacker either modulating or acquiring that noise; the last is perhaps the most practical. Many modern CPUs have their own internal true RNG based on this last principle, but you can also build a simple one—like mine above. It’s pretty crude.
I’ve tuned it so that you can plug it into the sound port of a computer, and then sample the sound. In the screen grab at the very start of my post, the output is in the audio range, and tapers off quickly above 20 kilohertz. You can see this in the top trace. There are no discernible patterns in the orange noise shown below.
Building a circuit like this may seem intimidating at first, but all you need is a ‘breadboard’ into which you can plug electronic components, a 9V battery, and those cheap components: connectors, capacitors, resistors, a couple of small transistors, and the source of the noise, the Zener diode shown on the left. That, and put the components in the right way around. This is a fun project, but if you want to use the random bytes of data, which are still normally distributed overall, you’ll need to do some manipulation after you sample them.
How this produces noise is quite interesting.5 There are said to be two mechanisms. At lower voltages, we have “shot noise” which arises from quantum tunnelling across the junction. Higher-voltage Zener diodes like the one used here produce something different, called “avalanche breakdown”.6 At about 6 volts, there’s a mixture of the two.
While many diodes are engineered precisely to minimise noise, noisy ones can be used to advantage. But how do we know that we’re dealing with truly random noise?
Okay, entropy
We are often cautioned not to mix up the mathematical concept of ‘entropy’ that we’re dealing with here, and the same word used by physicists in referring to thermodynamics. Here, we’re interested in Shannon entropy, which is both fascinating and useful.7
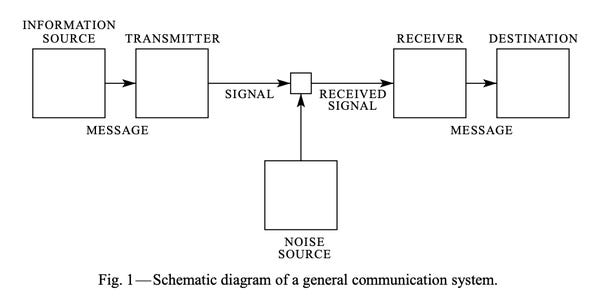
One of the gruntiest papers of the past century was written by Claude Shannon in 1948. It’s A Mathematical Theory of Communication, which pretty much kicked off the whole of information theory, and is still a good read. The above diagram is taken from his paper. Apart from the slight aside of defining the word ‘bit’ to represent a unit of binary information, Shannon’s main message is along these lines:
The entropy of a message transmitted across a noiseless channel is the absolute mathematical limit on how much you can compress that message. That is, the minimum number of bits into which you can squeeze the message.
In contrast, a sure fire mark of a crank—unless they are a fraud—is someone who claims that they have a “super compressor” that will allow lossless compression of huge amounts of data into a very tiny message. For example, in 2010, New Zealander Philip James Whitley was sentenced to just over 5 years in jail for fraudulently claiming that his company Near Zero Ltd had a radical new compression technology that would make investors billions. He took them for $5 million before it was pointed out in court that his claims were mathematically impossible.
A bit about compression
Consider an English text like the following from 1948:
“... semantic aspects of communication are irrelevant to the engineering problem. The significant aspect is that the actual message is one selected from a set of possible messages. The system must be designed to operate for each possible selection, not just the one which will actually be chosen since this is unknown at the time of design. If the number of messages in the set is finite then this number or any monotonic function of this number can be regarded as a measure of the information produced when one message is chosen from the set, all choices being equally likely. As was pointed out by Hartley the most natural choice is the logarithmic function.”
How would you make it shorter, while still preserving precisely the same content? Knowing that we generally represent letters in a computer using sequences of bits (‘A’ is commonly 01000001), we might reserve just a few bits for common letters like ‘e’, ‘t’ and ‘a’—the trade off being that less common letters would need more bits. We might use more complex approaches, for example coding common words like ‘the’, ‘message(s)’ and ‘number’ using shorter codes.
There are many smart compression tricks we won’t explore here. But Shannon’s key message is that there’s an optimal way to do this compression, below which we simply cannot go. If you squeeze more, then something busts out somewhere else! This in fact gives us a neat criterion for randomness—the sequence of numbers cannot be compressed any more.
In contrast, if there’s some sort of detectable pattern, then we can leverage that pattern to do some sort of compression. For example, someone might generate millions of numbers using the Mersenne Twister, but we could shorten this to (a) the initial state of the Twister when the first number was generated (~2.5k), and (b) the number of subsequent numbers generated. That’s it!
The limits of Diehard
“Nothing is random, only uncertain” [Gail Gasram, 1995]
There are some bright people out there, and few are brighter than cryptographers and their ilk, who are best characterised as mathematicians with deep-seated paranoia that is mostly justified. In 1968, George Marsaglia wrote a short paper called Random Numbers fall Mainly in the Planes. He looked at the primitive PRNGs of the day—linear congruential generators—and pointed out that they all have a flaw. If you look at them in multiple dimensions, then the numbers tend to line up (“in a relatively small number of parallel hyperplanes”). A direct consequence of this property is that it messes up Monte Carlo calculations. You can also spot this pattern, using suitable tests.
Nearly 30 years later, Marsaglia published an entire ‘Diehard’ suite of tests with one object in mind: finding patterned behaviour in data that claimed to be random.8 His suite (and the later “dieharder”) are potent at picking up deviations from randomness. There are also newer suites like PractRand, the rather complex TestU01, and NIST SP 800-22.
But there’s a problem. In fact, NIST SP 800-22 is now “considered harmful”. The problem here resonates nicely with my original definition of Science. There, we observed that just because something seems “true” cannot in any way guarantee some sort of Platonic realism.
Tomorrow, someone may come along and show that the pattern you thought was there is produced by some completely different mechanism. Our problem here is a twist on this idea: the randomness you thought was there, is actually highly patterned.
So, if you have (for example) a cryptographically secure PRNG, you simply cannot just plug the output into a suite of tests and then pronounce “It’s OK, really”. But we knew that already—from our insight into what the NSA did to NIST, back in 2006. Insecure PRNGs can seem pretty random, so you need to understand what’s under the bonnet. This is something best done by cryptographers, who are also the best people to recommend which CSPRNG you use. Provided, of course, that they’re not from the NSA, which unfortunately tends to attract the best and ultimately least principled cryptographers of the lot.9
Feeling paranoid yet? Don’t worry. In my next post, I’ll introduce the mind-projection fallacy. That’s a far greater concern! Failed randomness can erase your fortune, but the mind projection fallacy does something far worse. It erases your common sense.
My 2c, Dr Jo.
For those who criticise Ed Snowden’s actions, this revelation alone pretty much justifies what he did—and you need to examine your own blinkered state very carefully if you still can’t see this, or are in an active state of denial. Another bizarre component of the whole fiasco is that in 2006, Certicom tried to patent the NSA backdoor mechanism!
In fact, you don’t even need to know the probability density distribution you want—all you need is some function proportional to it. Built-in ‘random’ jumps (this is where you need the PRNG) let you successively create your distribution. This is particularly valuable when you’re dealing with modelling in many dimensions (e.g. hierarchical Bayesian models). At this point things become quite technical, e.g. Gibbs sampling.
Read the link to see the advantages. But quite because PCG is not a CSPRNG, it’s possible to recover its internal state if you have just 512 bytes of data. On average, you need a mere 20,000 hours of CPU time. If you’re interested, the very smart paper in that last link also explores the sometimes catastrophic consequences of choosing the wrong PRNG when you’re doing things like Monte Carlo simulation.
Although some groups of scientists have argued that there is measurable seasonal variation! It appears that this is not the case, instead arising in the calibration chain.
If you break your computer, that’s on you. I provide no guarantees whatsoever. Some would criticise the design because it uses higher voltages and perhaps more power than is needed. For more shot noise, design to use a Zener that runs on < 6 volts.
Thermal noise may ‘loosen up’ an electron-hole pair, and due to the voltage gradient, the two can separate. This can even result in a chain reaction-like phenomenon where these moving charges set others in motion—the avalanche.
More lies-to-children. Notably, NIST’s quantum voltage noise source is useful in accurately determining the Boltzmann constant, which ties into a whole lot of metrology including standards for measuring temperature with great precision. We’ve come to realise that Shannon entropy is just Boltzmann entropy without a commitment to a given physical system and its units. Here’s Shannon entropy:
And here’s Boltzmann—with ‘his’ constant kB:
Shannon’s use of “log” suggests that it’s flexible, and that we can use the natural logarithm, base 2 (for bits) and even base 10, for hominins with attitude and ten fingers.
Did you spot the ‘pattern’ hidden in the name ‘Gail Gasram’?
As noted above, modern processors provide a source of entropy that is then used to generate randomness for use in cryptography (RDRAND on Intel/AMD, RNDR on ARM, a distinct L4-based ‘secure enclave’ on Apple) usually via a ‘conditioning stage’. We do not know enough about their internals to determine whether there are built-in back doors. Now are you scared? (Oh, and there are other issues too).