Pidgin Bayes, with camels

(Mostly wrong, again)

Here’s a problem for you. Even if it’s vaguely familiar, you may still want to try working it out.¹

The probability that a woman between 40 and 50 years has breast cancer is 0.8%. If a woman has breast cancer, the probability that this will be successfully detected by a mammogram is 90%. If a woman does not have breast cancer there is a 7% probability of a false positive result on the mammogram.

A woman (age 45) has just tested positive on a mammogram. Is this likely to be breast cancer? What are the odds?

You may be slightly distressed when you learn that many doctors still get the answer wrong, often by an order of magnitude!

This is not my favourite Bayes-adjacent problem. I’ll come to that later. But first, breast cancer.

A naive take

Terry Pratchett has observed that camels make better mathematicians than people because, when confronted by tricky problems, humans almost always resort to counting on their fingers. Camels don’t have the luxury.²

I’m afraid that when confronted by this sort of problem, being far thicker than a Discworld camel, I too often resort to simple counting. Shall we give this a go?

1. Consider 1000 people.

2. The question is ambiguous, but we assume that the 0.8% is a point prevalence.³ So of our thousand, 8 will have cancer, now.

3. Ninety percent of those 8 will be successfully detected on mammography, so that’s about 7 of the 8 (7.2, actually, but for our crude finger counting, we disregard fractional fingers).

4. But hang on! Of the remaining 992, 7% or just under 70 will have a false positive.

5. So the chances of this being cancer are just one in eleven!

Is this the answer you got? We can work this out more formally, more generally and with fewer fingers using Bayesian reasoning. Camels would be proud of you.

Bayesian

As with all good things that are slightly difficult to understand, there’s often a risk that people who haven’t thought things through carefully enough will clothe Bayes in religious vestments. This is particularly easy to do given that the Reverend Bayes was a Presbyterian minister who dabbled in philosophy and statistics. First, a brief biographical note; then, the actual theorem; and yes, right at the end, we may touch on the religious aspects of Bayesianism.

Bayes in fact never formulated “his” theorem in a way that would be recognised by a modern Bayesian. He didn’t even publish his papers, which were put together after his death by Richard Price, and read to the Royal Society in 1763, two years after he died at the age of 59. A number of people came up with similar thoughts prior to him, and it was only later that Laplace (1774) saw the true generality of “Bayes’” theorem and how it can be used in problems of inference.

All of this doesn’t matter. The tool is potent. Bayes’ theorem easily answers questions along the following lines, and a lot more:

What is the probability that someone has a disease if they have a positive test for the disease, knowing three things: the probability of a positive test knowing they have the disease, the (population) likelihood that someone has the disease, and the overall probability of a positive test applied to that population?

As a bonus, the formula is pretty darn simple:

\(P\left(A|B\right)=P\left(A\right)\frac{P\left(B|A\right)}{P\left(B\right)}\)

Our breast cancer question seems pretty much designed to fit Bayes’ theorem—and of course it was. This is because this type of question is common, and perhaps a bit tricky. So let’s translate from mathspeak into English. All we really need to know apart from really basic maths is that P(x) means “the probability of x”, and P(x|y) translates as “the probability of x given that y is true”. Let’s try this.

If A is breast cancer and B is a positive mammogram, the likelihood that someone has cancer given a positive mammogram is just the probability that they have breast cancer, multiplied by the probability that they have a positive mammogram given that they have breast cancer, and divided by the probability that someone in this population has a positive mammogram.

It’s just easier to say with maths. First though, does this make sense? The number on the left (confusingly called the ‘posterior probability’) is going to go up if P(B|A) is greater, and if P(A)—the prevalence of breast cancer—goes up. It’s going to go down if P(B), the overall positive rate of the test, goes up. Makes some sense.

Let’s try some numbers, then. The tricky one is P(B):

\(P(B) = 0.9 \times 0.008 + 0.07 (1 – 0.008) = 0.07664\)

You can work this out from our finger-counting example above. We need to add up the contributions from the positives due to actual cancer and the false positives, to work out P(B). Now we can just plug in the numbers:

\(P\left(A|B\right)=0.008\frac{0.9}{0.07664}\simeq0.094\)

Our posterior probability (that this is cancer) is about 9%, or one in eleven.

We can make this even easier

There’s an even simpler way of looking at Bayes, if we use odds instead:

Posterior odds = original odds × likelihood ratio

In many medical circumstances, this is excessively cool. Let’s try another example. A doctor thinks the woman in front of her has a 40% chance of having substantial coronary artery disease. We can look up the likelihood ratio (LR) for a negative or positive test result, and pretty much just plug it in. Most exercise tests won’t have a good enough negative LR either to exclude or rule in the condition; while something like a CT coronary angiogram (CTCA) will perform better in ruling out substantial disease.

It’s easy to convert odds to a probability too: for an odds ratio of x:y, the corresponding probability is simply x / (x + y). So, for example, if the prior odds of coronary artery disease are 4:6 in favour and the LR for a negative effort ECG is 0.55, the posterior odds are 2.2:6, in other words, there’s still a 27% chance you’re sending someone out the door with substantial coronary artery disease if you stop there. A CTCA with its negative LR of 0.022 is clearly better—just do the numbers.

If you want to explore likelihood ratios further, here’s a decent explanation.

We can also make things far more complex

In the above, I’ve been a bit glib. I fudged P(B). It’s almost pidgin Bayes! And I didn’t explain how to derive the theorem (easily looked up, though). In contrast, one of my heroes ET Jaynes has written a 700 page book that looks into this in perhaps more detail than you would want to—Probability Theory: The Logic of Science. Brilliant, if you have the time. He explains why there is just one, consistent logical system for deduction, given very basic and sensible assumptions—and this system is indeed Bayesian. He even derives it from first principles: the idea behind Cox’s theorem. Jaynes also points out that we should really be saying things like:

\(P\left(A|BX\right)=P\left(A|X\right)\frac{P\left(B|AX\right)}{P\left(B|X\right)}\)

In other words, there is always some prior information X that we need to accommodate. He also frames things in terms of ‘sampling distributions’, and makes another really important point—that some people get confused by the labels ‘prior’ and ‘posterior’ into thinking that they refer to change over time (which is wrong) rather than the fact that they refer to a logical sequence of operations.

We’ll get back to Jaynes and examine his approach in some detail in a later post. In the meantime, if you’re really keen and have some maths, just get the book! We turn to my favourite, instead.

Still my favourite—Monty Hall with pigeons

You’ve likely come across the “Monty Hall” problem—largely because, way back in the 90’s, the very bright Marilyn vos Savant wrote about it in her “Ask Marilyn” column in Parade magazine. She got the answer right, but Parade was deluged with ‘errata’, usually generated by College Professors who got it all quite wrong—and almost never failed to belittle her and indicate that they had a PhD.

This is now almost an internet trope, but let’s have another look. We need to phrase the problem quite carefully, as the details count. It runs like this:

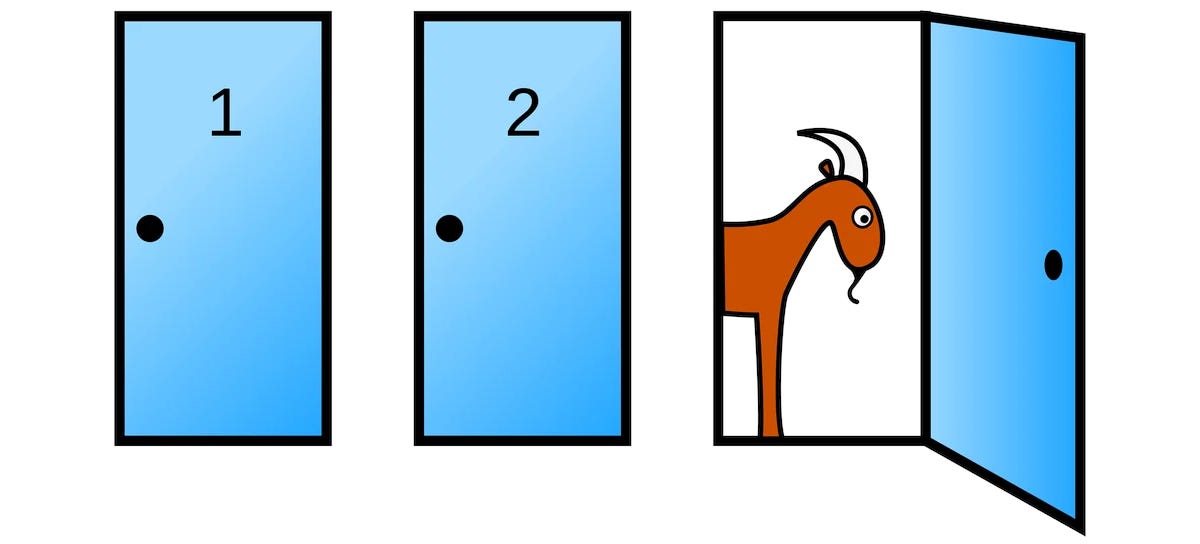
Monty Hall has set up a game show, with three doors set into the wall. Behind one is a swanky car⁴; both of the others hide scruffy goats. The contestant chooses a door, and then with great ceremony, Monty (as he always does) opens one of the doors to reveal a goat. Now (again, as he always does in this particular show) he gives the contestant the opportunity to switch doors before the final reveal. Should the contestant hold, switch, or simply remark that it doesn’t matter? (Above image from Odyssey).

The answer is clearly that the contestant doubles his chances if he switches—but this answer is only clear if you’re Marilyn, someone who has carefully thought through the problem, or Monty—who would never be daft enough to set up a real game where the switch is allowed. It is clearly not obvious to many smart correspondents with PhDs.

As with the children who outsmarted adults in my recent post, this scenario is easier to get right with Bayes’ theorem, especially if you think through the causal problem that Monty confronts.

If A is the door we pick, B is the door Monty first opens, and C is the door with the car behind it, then the corresponding directed acyclic graph that describes Monty’s decision is:

A → B ← C

From my previous post, you know that this is a collider! Monty’s action of revealing the goat (B) opens up the back door <grin>, creating a spurious association between A and C. So given the opportunity to change, we must switch. It’s equally important to realise that if the game is different, and Monty usually opens one of the doors randomly—with the possibility that he’ll spoil everything by revealing the car—then there’s no collider, and the subsequent probability of getting a goat or car is 50%, so there’s no reason to switch!⁵

Computer simulations also easily demonstrate the truth of the Monty Hall conundrum. If you want sophistication, there’s now free Python software called pyagrum with a full demonstration of the solution.

I have deliberately not explored the problem in greater depth for three reasons. If you know it already, I’m wasting your time; some rare people see it immediately; and the rest can have a lot of fun working through its counter-intuitive nature and arguing with themselves.

But I have one interesting factoid that blew me away the first time I encountered it. In 2011, Herbranson and Schroeder set up an “iterative Monty Hall problem” where subjects were repeatedly exposed to the three-door problem in a way that provided an appropriate reward—for either pigeons, or human participants. The pigeons rapidly found an optimal solution based on that 2/3 vs 1/3 advantage of switching; humans,⁶ like our PhD-wielding professors, didn’t.

It would seem that adult humans in particular are often a bit limited when confronted by unusual challenges that don’t fit their established notions. Properly applied, Science and Bayes can be a wonderful antidote to our closed-mindedness.

Religious vestments

We are all fallible. Even pigeons. In 1948, BF Skinner found that if presented with entirely random rewards—rewards with no relationship to their behaviour—pigeons would acquire and reinforce ‘superstitious’ behaviours!

Although Skinner’s explanation may be a bit glib, such vulnerabilities may well be part of what we are. There’s even a simple explanation. In order to respond to a stimulus, you need a threshold below which you don’t perceive that stimulus as worthy of a response. But there’s a catch—a payoff matrix that favours false positives. For many stimuli, such as not seeing the reward, or not seeing the lion, the results can be very severe—starvation, or a very well fed lion; but the odd false positive is often less consequential.⁷ So we are set up to perceive a fair number of rewards, threats and ultimately relationships that simply aren’t there.

It’s therefore not surprising that even Bayesian statisticians are prone to the problem of adopting ideas that are wrong, and indeed, ritualistic or even quasi-religious. As am I. When I first discovered Bayes’, the world took on a new rosy perspective—especially in the light of Cox’s theorem. Bayes is best! It seems all-wise, and everywhere applicable. And then I discovered the “Bayes Information Criterion” or BIC. Again, this appeared close to my heart, not only because it contained the magic word “Bayes” but also because of its promise—a well-reasoned way to test models for goodness of fit. You can find the best model!

Unsurprisingly, I was wrong. BIC is not that great. You see, a fundamental assumption here is that the list of models being compared contains the true (correct) model. Ding! The first time we examined Science, we concluded that, even if we somehow magically found “the true model”, we couldn’t be the slightest bit sure it was. So arguments that BIC is asymptotically correct as we approach an infinity of testing vanish in a “Poof” of genie-smoke.

And practically, other criteria for comparing models often just work better! For example, the Akaike Information Criterion and the Watanabe-Akaike Information Criterion. Why so? Because they don’t depend on the assumption of an absolute truth. They test fit relative to the other models.

It turns out that quite a number of Bayesians have similarly succumbed to “un-science”. They assume models, but don’t really bother to check them. This is in fact so common that it’s worth pretty much the entirety of my next post, where I will also pit Karl Popper against Edwin Thompson Jaynes, and find a satisfactory resolution, courtesy of some very smart statisticians who were not misled like me.

My 2c, Dr Jo.

1. This example is all over the web, in various flavours. I’ve used McCloy as a source; note the .DOC format.

2. Pterry has the wonderful ability to make humorous mathematical gobbledegook sound plausible. In Pyramids there’s this great quote:

The greatest mathematician alive on the Disc, and in fact the last one in the Old Kingdom, ... spent a few minutes proving that an automorphic resonance field has a semi-infinite number of irresolute prime ideals.

Far more pleasing than the BS we get from Deepak Chopra or Christopher Langan—and they claim to be serious! The camel picture was generated by Ideogram.

3. And not that 0.8% will get cancer between the ages of 40 and 50, which is more tricky. Then, we need to know things like how long the cancer is present before it declares itself, on average, and this opens up a can of worms.

4. Likely not a red Tesla.

5. The available information differs in the two scenarios. This example is explored in fine detail in Judea Pearl’s The Book of Why.

6. The usual human guinea pigs: undergraduates.

7. Thanks John Woodley for pointing out the lion/gazelle clip!